Monoidal adjunction
Suppose that 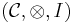 and
and 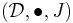 are two monoidal categories. A monoidal adjunction between two lax monoidal functors
are two monoidal categories. A monoidal adjunction between two lax monoidal functors
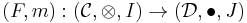 and
and 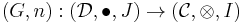
is an adjunction 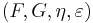 between the underlying functors, such that the natural transformations
between the underlying functors, such that the natural transformations
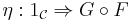 and
and 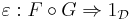
are monoidal natural transformations.
Lifting adjunctions to monoidal adjunctions
Suppose that
is a lax monoidal functor such that the underlying functor 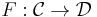 has a right adjoint
has a right adjoint 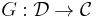 . This adjuction lifts to a monoidal adjuction
. This adjuction lifts to a monoidal adjuction 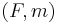 ⊣
⊣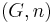 if and only if the lax monoidal functor
if and only if the lax monoidal functor 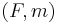 is strong.
is strong.
See also
- Every monoidal adjunction
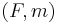 ⊣
⊣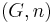 defines a monoidal monad
defines a monoidal monad 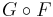 .
.